Parallel computation with helper threads in pqR
2013-06-23 at 5:00 pm 3 comments
One innovative feature of pqR (my new, faster, version of R), is that it can perform some numeric computations in “helper” threads, in parallel with other such numeric computations, and with interpretive operations performed in the “master” thread. This can potentially speed up your computations by a factor as large as the number of processor cores your system has, with no change to your R programs. Of course, this is a best-case scenario — you may see little or no speed improvement if your R program operates only on small objects, or is structured in a way that inhibits pqR from scheduling computations in parallel. Below, I’ll explain a bit about helper threads, and illustrate when they do and do not produce good speed ups.
First, helper threads can only be used to perform numeric computations that have been structured as “tasks”. Some primitive operations in pqR are done as tasks, some are not — re-writing code to do more operations in task procedures is one part of ongoing development of pqR. Note that whether or not some operation in pqR is structured as a task, and hence can potentially be done in a helper thread, is invisible to the user, apart from the effect on speed, and on output when the option to trace tasks is enabled. At present, operations done in tasks include arithmetic operations on vectors and matrices, matrix multiplies, matrix transpose, rowSums / colSums / rowMeans / colMeans, and some single-argument mathematical functions, such as exp and abs.
Second, pqR at present does not execute any single operation in parallel — if you add two matrices, pqR will use just one processor core to do that add. But pqR can execute two or more operations done as tasks in parallel. For example, if A, B, and C are large matrices, when pqR evaluates L <- list(A+B,A-C,f()), it may well perform the addition in parallel with the subtraction, and both in parallel with the computation of f(). This assumes that pqR has available at least two helper threads, to do the addition and the subtraction, along of course with the master thread, which can evaluate f().
You can see this happening if you enable tracing of what the helpers are doing. After starting pqR with the --helpers=2 option (and assuming you didn’t configure with --disable-helper-threads), you may see output like the following:
> options(helpers_trace=TRUE)
> A <- matrix(1.2,500,500)
> B <- matrix(3.4,500,500)
> C <- matrix(5.6,500,500)
> f <- function () sum(A)
> L <- list(A+B,A-C,f())
HELPERS: Task 1 scheduled: real_arithmetic(1,R250000:4a09020,R250000:594b5a0,R250000:3ac6aa0) PIPE_OUT PIPE_IN0 PIPE_IN1 PIPE_IN2
HELPERS: Task 2 scheduled: real_arithmetic(2,R250000:3e97400,R250000:594b5a0,R250000:4820b70) PIPE_OUT PIPE_IN0 PIPE_IN1 PIPE_IN2
HELPERS: Wait until R250000:4a09020 and R250000:3e97400 not being computed
HELPERS: Task 2 completed in helper 1
HELPERS: Task 1 completed in helper 2
HELPERS: Done waiting
> c (L[[1]][500,500], L[[2]][500,500], L[[3]])
[1] 4.6 -4.4 300000.0
After scheduling the addition and subtraction tasks, the master thread evaluates f(), and then goes on to create the list, which at present requires waiting until the addition and subtraction have finished, although in future, pqR will probably defer this wait until the list elements are actually used. Note that the trace output for a scheduled task includes descriptions of the variables operated on in terms of type, length, and address. (Note also that you may see different output, depending on how fast the computations in the helper threads went on your system.)
At this point, you may wonder what happens if f() changes A while the helper threads are using it to compute A+B and A-C. Well, pqR knows about this possibility, so the master thread will wait for all helper threads that are using A to finish their tasks before modifying it. Here’s an example, continuing from above:
> f <- function () { A[500,500] <<- 0; sum(A) }
> L <- list(A+B,A-C,f())
HELPERS: Task 1 scheduled: real_arithmetic(1,R250000:407f8b0,R250000:594b5a0,R250000:3ac6aa0) PIPE_OUT PIPE_IN0 PIPE_IN1 PIPE_IN2
HELPERS: Task 2 scheduled: real_arithmetic(2,R250000:4267d60,R250000:594b5a0,R250000:4820b70) PIPE_OUT PIPE_IN0 PIPE_IN1 PIPE_IN2
HELPERS: Waiting until R250000:594b5a0 not in use
HELPERS: Task 1 completed in helper 1
HELPERS: Task 2 completed in helper 2
HELPERS: Done waiting
> c (L[[1]][500,500], L[[2]][500,500], L[[3]])
[1] 4.6 -4.4 299998.8
Of course, having to wait until A isn’t used reduces the gain from parallelization. Here is a timing comparison with the two versions of f, and with helper threads disabled:
> options(helpers_trace=FALSE)
> f <- function () { A[500,500] <<- 0; sum(A) }
> system.time(for (i in 1:1000) L <- list(A+B,A-C,f()))
user system elapsed
3.820 0.004 1.375
> f <- function () sum(A)
> system.time(for (i in 1:1000) L <- list(A+B,A-C,f()))
user system elapsed
3.092 0.000 1.129
> options(helpers_disable=TRUE)
> system.time(for (i in 1:1000) L <- list(A+B,A-C,f()))
user system elapsed
1.500 0.000 1.502
The gain from parallelization in this example is a fairly modest factor of 1.502/1.129 = 1.33. This may be due to the time spent in memory allocation, which will not overlap with the computation of A-C in this example. (In fact, I notice that times for this example are highly variable depending on past memory allocations, which affect how often garbage collection is currently happening.)
The scope for parallel computation is pqR is greatly expanded when tasks can use pipelining. Most, but not all, of the pqR task procedures can produce output a bit at a time, and can accept input a bit at a time before their inputs have been fully computed. This allows expressions such as (A+B)*(A-C) to be done in parallel using three helper threads, one each for the addition, subtraction, and multiplication, with the last running concurrently with the first two, taking pipelined input.
Variables in pqR can contain objects that are in the process of being computed, so code like X<-A+B; Y<-A-C; X*Y can also result in the addition, subtraction, and multiplication being done in parallel.
Given this last feature, one has to be careful when trying to test how much gain there is from helper threads in pqR — code like for (i in 1:1000) X <- A%*%B might show a huge speed up, but only because pqR never has to wait for the results, since they’re never used! In my R speed tests, the “hlp-” tests are designed for testing the helpers facility, and the “prog-” tests are also valid, though most of them operate only on small objects and so offer little scope for parallelization.
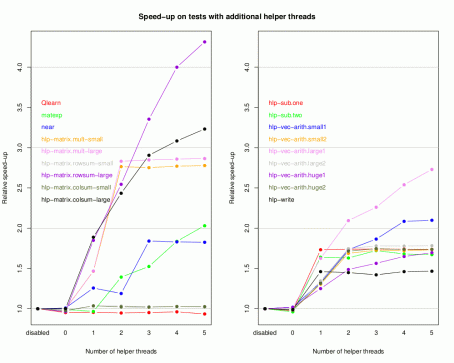
Here is a plot showing the speed-up obtained using helper threads on the “hlp-” tests, as well as three of the “prog-” tests (click to expand):
The times are for a system with one Intel X5680 processor with six cores. The “Qlearn” test operates only on small objects, so it shows what overhead there is using helper threads when they are of no use. There is also little gain when rowSums and colSums are applied to two fairly small (200×200) matrices at once, perhaps because computation time is dominated by the overhead of the R portion of these functions. The other tests show varying degrees of benefit from using helper threads.
The use of helper threads in pqR is still being developed, and I expect further significant improvements in performance. One potentially large improvement is to use multiple helper threads for a single operation, when the helper threads are not all otherwise occupied. It should be possible to do this while still supporting pipelining, if the multiple threads process interleaved blocks of the data.
The implementation of helper threads uses a general-purpose “helpers” library that I have developed, which may be useful to implementors of other languages.
Entry filed under: Computing, R Programming, Statistics, Statistics - Computing. Tags: pqR.
3 Comments Add your own
Leave a reply to Manju Cancel reply
Trackback this post | Subscribe to the comments via RSS Feed
1. Comparing the speed of pqR with R-2.15.0 and R-3.0.1 | Radford Neal's blog | 2013-06-24 at 11:40 pm
[…] speeds up simple real programs in my post announcing pqR, and to show the speed-up obtained with helper threads in pqR on systems with multiple processor […]
2. Manju | 2013-06-30 at 9:52 am
How could this be used with Big Data operation
3. Radford Neal | 2013-06-30 at 11:16 am
Well, if you have lots of data, processing it faster may be a high priority, so pqR could be a big help. The current and forthcoming improvements in pqR that avoid unnecessary duplication of objects could also be very important if your objects are a Gigabyte or more in size. On the other hand, pqR is based on R-2.15.0, and shares its limit of no more than about 2 billion elements in a vector (that’s 16 Gigabytes for a typical vector of real values). In R-3.0.x, you can have larger vectors (with some limitations).