Critique of “Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period” — Part 2: Proxies for incidence of coronaviruses
2020-06-17 at 8:55 pm 6 comments
This is the second in a series of posts (previous post: Part 1, next post: Part 3) in which I look at the following paper:
Kissler, Tedijanto, Goldstein, Grad, and Lipsitch, Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period, Science, vol. 368, pp. 860-868, 22 May 2020 (released online 14 April 2020). The paper is also available here, with supplemental materials here.
In this post, I’ll start to examine in detail the first part of the paper, where the authors look at past incidence of “common cold” coronaviruses, estimate the viruses’ reproduction numbers (R) over time, and use those estimates to model immunity and cross-immunity for these viruses, and seasonal effects on their transmission. The results of this part inform the later parts of the paper, in which they model the two common cold betacoronaviruses together with SARS-CoV-2 (the virus for COVID-19), and look at various scenarios for the future, varying the duration of immunity for SARS-CoV-2, the degree of cross-immunity of SARS-CoV-2 and common cold betacoronaviruses, and the effect of season on SARS-CoV-2 transmission.
In my previous post, I used the partial code released by the authors to try to reproduce the results in the first part of the paper. I was eventually able to do this. For this and future posts, however, I will use my own code, with which I can also replicate the paper’s results. This code allows me to more easily produce plots to help understand issues with the methods, and to try out alternative methods. The code (written in R) is available here, with GPLv2 licence. The data used is also included in this repository.
In this second post of the series, I examine how Kissler et al. produce proxies for the incidence of infection in the United States by the four common cold coronaviruses. I’ll look at some problems with their method, and propose small changes to try to fix them. I’ll also try out some more elaborate alternatives that may work better.
The coronavirus proxies are the empirical basis for the remainder of paper.
The paper constructs these coronavirus proxies in two stages. First, a proxy is constructed for the incidence of “Influenza-Like Illness” (ILI), which may be actual influenza or some other infection causing similar symptoms. Second, this proxy is multiplied by the percent of tests on patients with ILI that were positive for each of the common cold coronaviruses, to produce proxies for incidence of each of these coronaviruses.
The proxy for Influenza-Like Illness
The data on Influenza-Like Illness (ILI) in the U.S. comes from the CDC FluView site. A proxy for ILI can be obtained by combining data on the total number of patient visits to participating providers with the number of these visits that are for ILI. The FluView site has the following warning:
The number and percent of patients presenting with ILI each week will vary by region and season due to many factors, including having different provider type mixes (children present with higher rates of ILI than adults, and therefore regions with a higher percentage of pediatric practices will have higher numbers of cases). Therefore it is not appropriate to compare the magnitude of the percent of visits due to ILI between regions and seasons.
We can’t let this warning stop us from doing anything, but it may be worth keeping in mind. (Kissler, et al. don’t mention this warning.)
The FluView data is by week, and contains the number of providers that week, the total number of patient visits, the total visits for ILI, and an age breakdown for ILI visits. It also contains the percentage of visits that are for ILI, which is simply the number of ILI visits divided by the total number of visits, and a “weighted percentage” of visits that are for ILI, which “is calculated by combining state-specific data weighted by state population” (see here).
The Kissler et al. paper simply uses this weighted percentage of ILI visits as their proxy for ILI. They refer to a paper by Goldstein et al. for discussion of the conditions under which this proxy will be proportional to the actual incidence of ILI, and when multiplied by the percentage of tests on ILI patients that are positive for a particular virus, will give a valid proxy for incidence of that virus:
This proxy would be a perfect measure (up to a multiplicative constant) of the incidence of infection with a particular strain if the following conditions were met: (i) the fraction of ILIs that result in medical consultations, while possibly varying by strain, does not vary by year or by week; (ii) the numbers of physician visits for all causes in the sentinel practices were consistent from week to week during the season; (iii) the sentinel practices were representative of the full population; and (iv) viral testing, which is conducted in a separate system, was performed on isolates representative of those obtained from patients consulting the sentinel practices for ILI.
One cannot, of course, expect the conditions above to be exactly satisfied. Goldstein et al. remark that “Nonetheless, we take this proxy measure as the best relative measure of influenza strain-specific incidence that can be calculated from surveillance data”. (The Goldstein et al. paper deals with influenza strains rather than coronaviruses, but the technique used is the same.)
In the Kissler et al. paper, condition (iii) it is not actually necessary — it would be sufficient for the proxies to be representative of some stable and reasonably diverse portion of the U.S. population, since that would be equally informative regarding the characteristics of the virus. So it is not clear that the weighted percentage used by Kissler et al., which I’ll call proxyW, is superior to the unweighted percentage, which I’ll call proxyU. It could be worse, if the weighting procedure produces a greater violation of condition (iv).
Condition (ii) is an unreasonable assumption even in an idealized world without all the other complications that exist in reality (such as holidays, as discussed below). For it to be true in conjunction with condition (i), it would be necessary for visits to physicians for other reasons to go down whenever visits for ILI go up. This could only be true if physician visits are rationed to a fixed number per week, and visits for ILI are prioritized over visits for other reasons. This seems quite unlike how the U.S. health care system operates. And in the data, the total number of physician visits per week in fact varies substantially.
A less unreasonable assumption would be that the number of non-ILI physician visits per week is constant. Then the appropriate ILI proxy — which I’ll call proxyA — would be the ratio of ILI visits to non-ILI visits. Of course, the number of non-ILI visits is not really constant, but this proxy could still be good if the variation in number of non-ILI visits is due to reporting issues, such as providers commencing or ceasing data reports to the CDC, and these issues affect ILI visits in proportion. Also, if the number of non-ILI visits varies for other reasons, perhaps these reasons are unrelated to ILI visits, and so just add unbiased noise to the measurements.
In the actual data, the percentage of visits due to ILI is never greater than about 8%, and consequently the difference between proxyU and proxyA is not large. But use of proxyU (or proxyW) will tend to diminish the size of peaks of incidence — for instance, an increase in proxyU from 1% to 8%, a factor of 8, corresponds to an increase in proxyA from 1/99=1.01% to 8/92=8.70%, a factor of 8.6.
ProxyW, proxyU, and proxyA all have other problems, one of which can be seen for proxyW by plotting its value over the time period used by Kissler et al. (click for larger version):
The red vertical lines indicate the start of CDC’s “flu season” (week 40); the green lines indicate its end (week 20 of the next year). The grey vertical lines are just before the weeks of the 4th of July, Labor Day, Thanksgiving, Christmas, and New Year’s Day holidays (note that CDC weeks start on Sunday). One can see that the weeks of Thanksgiving, Christmas, and New Year’s Day (the last three holidays of a year) have systematically higher values for proxyW (the same is true for proxyU and proxyA). This is most clearly seen in the plot at the end of 2015, but is true for all years (with one or two unclear cases).
Since the values immediately before and after these holidays are lower (noting that Christmas and New Year’s Day are always in consecutive weeks), it is clear that these jumps are not due to actual high levels of ILI during these holiday weeks. This may seem counter-intuitive — do people really decide to spend their holidays visiting their doctor about an illness that they would not have bothered getting attention for if they weren’t on holiday? They don’t. A log plot of ILI visits shows that there is actually a tendency towards fewer ILI visits in holiday weeks, especially for Thanksgiving (click for larger version):
The reason for the higher proxy values in holiday weeks is that those weeks have an even greater decrease in non-ILI visits:
The ranges for the vertical scale in these logarithmic plots are the same, so one can see that the holiday decreases in non-ILI visits are larger than the decreases in ILI visits — perhaps people don’t visit doctors for routine reasons when on holiday, but are more inclined to do so when actually sick. This is the reason for the spurious increase in the percentage of visits due to ILI on holidays.
I’ve tried correcting the holiday problem with a simple fudge — replace each holiday value with the linear interpolation from the two adjacent non-holiday values. I call the modified proxies proxyWX, proxyUX, and proxyAX. Here is how this fudge changes the values for proxyA (click for larger version):
The pink dots above are the logarithms of the proxyA values; the black lines from them go to the corresponding values for proxyAX. This fudge seems to have improved the situation with Thanksgiving, Christmas, and New Year holidays, though one might wonder whether the peak at Christmas 2014 has been flattened too much.
There could be other problems, however. A more general framework could view the number of reported cases of ILI in some week as being the result of three factors:
- The actual incidence of ILI that week.
- The tendency in that week for people with ILI to visit a physician.
- The availability to people with ILI that week of physicians who report ILI to the CDC.
To infer (1) from the number of reported cases of ILI, we need first to somehow infer (2) and (3), or at least their combined effect.
ProxyA (the ratio of ILI visits to non-ILI visits) is based on two assumptions. First, that (2) is the same for all weeks. Second, that (3) can be estimated by the number of non-ILI visits — that is, that the number of non-ILI visits can be taken as indicative of the availability to potential ILI patients of physicians who report to the CDC, or to put it another way, that the number of non-ILI visits is proportional to the probability that a patient who would like to visit a doctor due to ILI will visit one of the physicians who reports visits to the CDC.
We see that on holidays this second assumption is not correct, since the number of non-ILI visits drops substantially, but providers who report to the CDC seem to be as available (or nearly as available) to patients with ILI as on other days. It’s possible that on holidays there is a small decrease in the availability for ILI patients of providers who report to the CDC. This cannot easily be distinguished from a small decrease those weeks in the tendency of people with ILI to visit a doctor. But distinguishing seems unnecessary as long as the total effect can be estimated, which is what proxyAX tries to do, in a crude way.
A more elaborate approach to creating an ILI proxy
A less crude method, which might also be able to correct problems other than holidays, is to build a model for ILI visits whose components can be identified (under some assumptions) as indicative of actual ILI or not. For this to work well, a model for non-ILI visits may also be needed, some of whose components can be identified (under more assumptions) as being indicative of the degree of availability of providers reporting to the CDC.
I’ll start with a model for non-ILI visits. A major component of this model will be the number of providers who report to the CDC each week, the log of which is plotted below:
Most notable is the sudden jump at the start of CDC’s official “flu season” (red line, week 40 of the year). Presumably, more providers are recruited at this time. Puzzlingly, although there is a corresponding drop at the end of the flu season (green line, week 20), it is much smaller. Providers recruited at the start of the flu season seem to drop out gradually. Perhaps many just get tired of the whole thing after a while (but if that’s the reason, it’s odd that apparently they all start doing it again next flu season). A more troubling possibility is that providers drop out because they have seen little or no ILI, which would bias the results, in the direction of ILI seeming to decline more slowly than it actually does.
In 2014 and 2017, there’s also a small jump after Labor Day. I can’t think of a reason for this, unless some providers are just eager to start flu season reporting.
These jumps in the log of the number of providers correspond to jumps in the log of the number of ILI and non-ILI visits, but the jumps in visits are smaller.
As a first attempt at modelling the log of the number of non-ILI visits, I fit a regression model with the log of the number of providers as a covariate, along with a spline with nine degrees of freedom to capture the trend over the five-year time period. Here is the fit (in blue) along with the data points:
Here are the residuals for this model:
The effect of holidays (4th of July, Thanksgiving, Christmas, and New Year’s Day) are clearly visible in the residual plot. The next model adds indicators for these holidays as covariates. They are 1 the week of the holiday and 0 otherwise (except that the Christmas indicator is more complicated, being split between early years and later years, and being partially active for the week before when Christmas is early in the week):
Here are the residuals for this model:
One can see a strong seasonal effect in which the number of visits grows in September, just before the official start of flu season (marked by the red line). Perhaps this relates to the end of summer vacations, or the start of school. There’s then an abrupt drop immediately after the start of flu season, presumably because the mix of providers suddenly changes. Other seasonal patterns also seem to be present.
To model a seasonal effect, I added covariates of the form sin(2πfy) and cos(2πfy), where y is a continuous indicator of years since the start of the period, and f is 1 or 2. These covariates are the initial terms of a Fourier series representation of a periodic function. I also added the week within the flu season and its square as covariates, allowing for the abrupt change when flu season starts.
Here is the fit of this model:
Here are its residuals:
This seems to be about as good a model as we can expect to get for non-ILI visits.
One way we might try to use this model is to use only its intercept, spline, and log(providers) components to predict non-ILI visits, and take the ratio of ILI visits to these predictions for non-ILI visits as a proxy for ILI incidence. I call this proxyB. It will have less noise than proxyA because it omits residuals in the predictions for non-ILI visits. It handles the holiday problem fairly well by omitting the holiday component in the non-ILI predictions. By omitting the seasonal component in the predictions, it avoids mis-characterizing seasonal variation in non-ILI visits as seasonal variation in incidence of ILI.
However, proxyB has some serious problems. Here is how it compares to proxyAX (click for larger version):
ProxyB systematically moves points (compared to proxyAX) in a way that introduces a discontinuity where flu season starts (the red line). It also seems to be doing something wrong in January of 2016.
We might hope to do better using a model for the log of the number of ILI visits. As covariates, we can again use a spline, the log of the number of providers, and the indicators of holidays. However, I’ll use a spline with more knots (one at the start of each month), which can model seasonal effects as well as long-term trends. (Unlike for non-ILI visits, the seasonality for ILI visits is not firmly fixed to the calendar — the time of the peak varies in different years by several weeks — so a Fourier representation of seasonality that is common to all years is not appropriate.)
Here is the fit for this model of log ILI visits:
Here are its residuals:
This residual plot doesn’t reveal any serious problems with the model (a little heteroskedasticity, but we can tolerate that). To use it to produce an ILI proxy, we need to decide what components of the model to retain. The variation due to holidays seems like it can’t be indicative of real change in ILI. The variation due to change in the number of providers also seems irrelevant. So we’re left with the spline fit and the residuals:
I call this proxyC (after applying an ad hoc overall scaling factor to get it to roughly match the scale of other proxies). Here’s how it compares to proxyAX (click for larger version):
If one looks at the time at and just after Christmas / New Year’s Day, ProxyC seems to do better than proxyAX in 2016/2017, 2017/2018, and 2018/2019, but worse in 2014/2015 and 2015/2016, assuming that curves that are smoother here are more likely to be correct.
One can also see a general tendency for proxyC to lower the minimum incidence in summers before 2018, and to raise the peak incidence in winter in 2018 and 2019.
Finally, here’s the fit of another model for log of the number of ILI visits, in which the residual from the final model above for the log of the number of non-ILI visits is included as a covariate (in addition to those used in the ILI visits model above):
This doesn’t look much different from the fit for the first model of ILI visits, but there is a significant improvement, with the estimated standard deviation of the residuals declining from 0.05106 to 0.04703. The regression coefficient for the non-ILI model residuals in the ILI model is 0.809, so most the the residual variation in non-ILI visits seems to be indicative of accessibility of providers to potential ILI patients, rather than variation in demand for non-ILI medical services.
I use the spline fit and residuals from this model to create another ILI incidence proxy, which I call proxyD (after again applying an overall scale factor to make it roughly comparable to the other proxies). Here’s how proxyD compares to proxyC (click for larger version):
The changes in proxyD are small, but seem to be desirable, assuming that lesser discontinuity is more likely to be correct.
ProxyD seems to be the best of these proxies, with proxyAX being a much simpler alternative that’s worth comparing against. To conclude this section, here is how proxyW, used by Kissler et al., compares to proxyD:
One can see the holiday problem with proxyW. There’s also a general tendency for proxyW to be lower than proxyD in 2018 and 2019. This seems related to the rise in the number of providers reporting to the CDC those years, which went along with a rise in the number of non-ILI visits per provider in those years, and a decrease in the number of ILI visits per provider (at least in some periods). The warning from the FluView site quoted above may be relevant here — the additional providers reporting to the CDC may serve a population that makes relatively more non-ILI visits.
The proxies for coronavirus incidence
The Kissler et al. paper uses their ILI proxy to create proxies for the four common cold coronaviruses — NL63, 229E, OC43, and HKU1. [ Note: The R code uses the name E229 instead of 229E, since the latter is not a valid R identifier. ]
This is done very simply in the paper — their proxy for incidence of a virus is just their proxy for ILI (proxyW, weighted percent ILI among all visits) times the percent of tests on ILI samples that were positive for that virus.
Here’s what their proxies look like (click for larger version):
These plots don’t look too bad. But look at these proxies on a log scale:
OC43 still looks OK, but the others, especially HKU1, have a lot of noise in the smaller values. Some of the values are zero, which are shown above as dots at the bottom. Note that it is the logarithmic plot that is relevant to assessing how variability will affect the later estimation of R values.
After some investigation, I decided that one thing that needs to be done to get good results is to adjust a few outliers. There is no information available about what is responsible for these extreme values. They could be testing or reporting anomalies, or they could be correct but unrepresentative (eg, due to positive tests for all people in one large family).
Here are plots of the log of the percent positive tests for each virus, with points I regard as outliers in red, and with lines to where I moved them, with zeros again plotted at the bottom (click for larger version):
The outliers were replaced by the average of the four nearest points, except that for the NL63 outlier, which is zero, this average was divided by 1.3, to reflect the possibility that the zero value is not entirely spurious.
I also replaced all the zero values with the minimum non-zero value for the series, divided by 1.3 to reflect that while a zero measurement cannot represent an actual zero incidence, it is evidence that the incidence then was lower than the non-zero measurements.
Proxies based on the percentages after these adjustments for outliers and zeros have an “o” appended to their name. Here, for example, is log proxyAXo for the four viruses (click for larger version):
These proxies do not have extreme points, but are still rather noisy. As I’ll discuss in a later post, Kissler, et al. handle noise by averaging their final estimates for R over three weeks. It seems better to instead reduce noise at this stage.
The approach I’ve taken is to re-express the proxy for a virus as the product of the ILI proxy, the total of positive test percentages for all four viruses, and the ratio of percent positive tests for that virus to the total. If no smoothing is done, this is the same as the product of the ILI proxy and the percent positive tests for that virus. But the effect of smoothing the total and/or the ratios to the total is different from smoothing the percentages of positive tests. (Outliers and zeros are adjusted before these procedures.)
I create two new sets of proxies by smoothing the ratios of percent positive for each virus to the total percent positive, done by applying a filter with impulse response (0.2,0.6,0.2) either once or twice. I name these proxies by appending “s” or “ss” to the name of the ILI proxy. Here is log proxyAXss:
I’ve also created proxies based on smoothing with splines. Here are the spline fits for the logits of ratios of percent positive to total percent positive (click for larger version):
Here is the spline fit for the log of the total percent positive:
The rationale for this approach, smoothing the total and the ratios separately, is that the total captures a good chunk of the variability but shows a more regular pattern, with less noise, than the individual percent positive series. So modelling the total separately could be beneficial. I haven’t done any extensive tests to validate this intuition, however.
I used these spline fits to create two new versions of the coronavirus proxies. The “m” versions use the spline fit for the ratios but the actual values for the totals. The “n” versions use the spline fits for both. Here is proxyDn:
Noise has certainly been reduced. One might of course wonder whether some real features have been smoothed out of existence.
Future posts
In my next post, I’ll discuss how the coronavirus incidence proxies are used in the paper to produce estimates for the reproduction numbers (R) of these viruses, for each week from mid-2014 to mid-2019. This will be followed by a post discussing how the paper models these R values, in terms of immunity and seasonal effects. As above, I will discuss problems with the methods in the paper, and alternatives that might be better.
After those posts, I’ll go on to discussing the later parts of the paper, which are intended to provide some policy guidance.
Entry filed under: COVID-19, R Programming, Science, Statistics, Statistics - Computing, Statistics - Nontechnical.
6 Comments Add your own
Leave a comment
Trackback this post | Subscribe to the comments via RSS Feed



























1. ecoquant | 2020-07-01 at 12:02 am
Tremendously detailed and complete analysis! I really enjoyed the careful dissection and modeling of ILI and non-ILI.
On the seasonal, rather than use early terms of Fourier series, might do as done in state space modeling and declare that for any seasonal component , for
, for  , with
, with 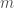 samples in a season, then:
samples in a season, then:
This would liberate, too, from the phase restrictions which and
and 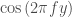 impose.
impose.
2. Radford Neal | 2020-07-01 at 9:36 am
You’re thinking of modelling seasonality by explicit indicators for each time point in a season? Then it would make sense to impose the constraint that they sum to zero, or ease of interpretability if no other reason. But for this data, there are only 5 seasons, so some scheme that imposes smoothness on the
indicators for each time point in a season? Then it would make sense to impose the constraint that they sum to zero, or ease of interpretability if no other reason. But for this data, there are only 5 seasons, so some scheme that imposes smoothness on the  seems necessary.
seems necessary.
Allowing a linear combination of sin and cos doesn’t impose phase restrictions, since you can get a sine wave with any phase that way. In fact, even in a Bayesian context, this scheme works fine, since independent Gaussian priors for the regression coefficients on the sin and cos components results in a uniform distribution for the phase of the combined wave.
Gaussian priors for the regression coefficients on the sin and cos components results in a uniform distribution for the phase of the combined wave.
3. ecoquant | 2020-07-01 at 10:01 am
Actually, regarding , I meant
, I meant
where is the observed count or index at time point
is the observed count or index at time point  ,
,  is the periodic,
is the periodic,  is some zero mean noise, and
is some zero mean noise, and  is a deterministic function of
is a deterministic function of  which describes the upramp/downramp of LI visits, probably a ratio of sums of exponentials. Over the course of a season the net contribution from
which describes the upramp/downramp of LI visits, probably a ratio of sums of exponentials. Over the course of a season the net contribution from  is zero.
is zero.
On the second point, okay, but per “Unlike for non-ILI visits, the seasonality for ILI visits is not firmly fixed to the calendar — the time of the peak varies in different years by several weeks — so a Fourier representation of seasonality that is common to all years is not appropriate”, mightn’t there be departures season by season even for ILI? Or does the uniform distribution for phase take care of that? And if it doesn’t, why doesn’t it take care of it for non-ILI?
4. Radford Neal | 2020-07-01 at 10:29 am
Yes, the more detailed model you show above was what I was thinking of. For this data,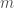 would be 52, which gives too many
would be 52, which gives too many  to fit with only 5 years of data, unless they are constrained or smoothed in some way.
to fit with only 5 years of data, unless they are constrained or smoothed in some way.
I think you’ve reversed “ILI” and “non-ILI” in your second paragraph. The seasonality of non-ILI visits seems to be tied to calendar events, such as the start of school. The ILI seasonality seems to be tied to virus dynamics, which has a general seasonality, but with peaks that aren’t precisely timed by the calendar (varying by several weeks, perhaps because of the weather that year, or whatever). In both cases, there could be a bit of the other kind of seasonality, but putting in both kinds for both ILI and non-ILI visits seems too complicated.
The ability of sums of sin and cos to produce any phase is important to getting the calendar sort of seasonality to have peaks in the right places, but doesn’t help if the peaks move around from year to year. One could build a model with an AR(2) component (which can exhibit oscillations of around some period, but not precisely fixed), but that seems too elaborate in this context.
5. Liam | 2020-07-02 at 12:38 am
Hi Radford, thanks so much for sharing this. I have no medicine and statistics background so I don’t quite understand this, but I am wondering if you think that the covid-19 will happen every year on a significant scale in the future. Thanks so much!
6. Radford Neal | 2020-07-02 at 8:11 am
That’s the sort of question that the later parts of the Kissler, et al. paper try to answer. I’ll be discussing those parts in a future post. I haven’t finished examining what they did, so I can’t say exactly what I’ll conclude about that.
Leaving aside the particulars of this paper, though, I think it’s reasonable to see COVID-19 staying around as a seasonal (in temperate regions) disease as one possible scenario. If so, it might also evolve to become serious (though of course in many people it is already not serious). I think it’s pretty hard to make definite predictions.