Evaluation of NUTS — more comments on the paper by Hoffman and Gelman

Here is my second post on the paper by Matthew Hoffman and Andrew Gelman on “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo”, available from arxiv.org. In my first post, I discussed how well the two main innovations in this “NUTS'” method — ending a trajectory when a “U-Turn” is encountered, and adaptively setting the stepsize — can be expected to work. In this post, I will discuss the empirical evaluations in the NUTS paper, and report on an evaluation of my own, made possible by the authors having kindly made available the NUTS software, concluding that the paper’s claims for NUTS are somewhat overstated. The issues I discuss are also of more general interest for other evaluations of HMC.

The scripts used for the empirical evaluations in the NUTS paper are not included with the NUTS software, so in some respects I’m not certain what was done, but the description in the paper is fairly complete.

The foundation for any empirical assessment of MCMC methods is some way of estimating how good the MCMC estimates are, which could be the autocorrelation time, or the variance of the estimate, or the effective sample size (ESS, the equivalent number of independent points). The NUTS paper uses autocorrelation time, from which they compute the effective sample size.  They estimate autocorrelations using means and variances found from a very long run, not from the run being evaluated, which avoids one possible source of drastically wrong results in such evaluations. (For the zero-mean multivariate normal example I discuss below, they presumably plugged in the true mean of zero and the true variances, rather than use a long run.) As their measure of overall performance for a sampler, they used its worst performance (in terms of autocorrelation time or ESS) over all variables (looking at both mean and variance estimates for these variables). Focusing on the worst estimate seems reasonable in a way, but looking at only this one number could be misleading if the estimate that is worst is different for different samplers.

One aspect of their evaluation (as described in the paper) is incorrect. In the Appendix, they say that they estimate autocorrelation time by summing autocorrelation estimates at all lags up to the first lag at which the autocorrelation estimate is less than 0.05. Since the true autocorrelation can sometimes be negative, this is not valid, in general — it would be for some simple random-walk Metropolis methods, for which autocorrelations are all positive, but not for HMC, for which negative autocorrelations are quite possible. However, for reversible methods (which includes HMC), the sums of consecutive pairs of autocorrelations are always positive. This provides the basis for a similar approach that is valid. See here for a review and assessment of this and other approaches to estimating autocorrelation time.

Assuming that this is an error in the actual code (not just the paper), it could affect the empirical results quite a bit, but I’ll have to ignore this possibility in the remaining discussion.

The first distribution that Hoffman and Gelman test NUTS on is a 250-dimensional multivariate normal distribution with mean zero and a covariance matrix randomly drawn from an inverse Wishart distribution. They claim that NUTS performs better on this distribution than HMC (by a factor of about three) even when HMC is optimally tuned. This seems strange, since NUTS is just an automated way of tuning HMC. As I’ll show below, this claim is indeed likely to be due to deficiencies in the experimental methodology.

Due to rotational invariance, performance of HMC on a multivariate normal is determined by the set of eigenvalues of the covariance matrix, with the inherent difficulty of the problem being proportional to the square root of the ratio of the largest eigenvalue to the smallest eigenvalue. This is the ratio of the standard deviation in the least confined direction to the standard deviation in the most confined direction, and should be roughly the number of leapfrog steps in a trajectory of optimal length, using the optimal stepsize. (Performance by Hoffman and Gelman’s metric isn’t quite rotationally symmetric, however, since they look only at autocorrelation times for the 250 variables, not all linear combinations of them.) The evaluation of HMC and NUTS on this distribution would be much more informative if the eigenvalues of the covariance matrix were reported, and if the number of leapfrog steps in HMC trajectories (not just the product of stepsize and number of steps) were reported.

I’ll return below to the multivariate normal example, but first I’ll mention the other distributions on which HMC and NUTS are evaluated in the paper. Two of these other distributions are posterior distributions for logistic regression models. The results on these distributions are more what one might expect — NUTS performs about as well as HMC with optimal tuning. One slightly strange phenomenon is visible in the results presented in Figure 6, however. For both logistic regression problems, the performance of HMC drops drastically as the trajectory length is increased from the optimal value to a value larger by a factor of 1.5. I would expect a more gradual decline in efficiency.  It would be nice to know why this occurs.

The last distribution they evaluate NUTS and HMC on is the posterior distribution for  a stochastic volatility model.  Here again, they claim that NUTS performs better than HMC, even when the latter is optimally tuned. I’m not sure what is going on here, but one thing I notice in the lower left plot in Figure 6 is that the performance of NUTS seems to be bimodal — some of the runs are assessed as being three times better than the best HMC runs, but others are assessed as being worse. All I can think of to explain this bimodality is that the adaptive stepsize selection might be reaching either of two stable values. The advantage of some NUTS runs over the best HMC runs might be explained by the same factors that lead to this result for the multivariate normal.

Since the actual multivariate normal distribution used in the paper isn’t reported, I’ll look at performance of NUTS and HMC on another multivariate normal, the same 30-dimensional multivariate normal distribution that I used in my previous post, in which the 30 components are independent, with standard deviations of 110, 100, 1.1, 1.0, and 26 values equally spaced between 8 and 16. This may in any case be a better demonstration example than one in which the standard deviations are chosen randomly.

I used the NUTS software for these experiments, with automatic stepsize adaptation for both HMC and NUTS (the adaptation always converged to a reasonable value of around 1.63 for HMC and around 1.73 for NUTS). I did 10,000 burn-in iterations, followed by 250,000 sampling iterations, which I divided into 400 batches of size 625. I estimated the mean of each variable and the second moment of each variable (equal to the variance, since the true mean is zero) for each of the 400 batches, and looked at the variance of these batch estimates as a measure of the performance of the sampler, not accounting for computation time yet. I then multiplied the variances of these batch estimates by the number of gradient evaluations for the whole run to get figures of merit that account for computation time. I used this Matlab script for these experiments (and then moved the results to R for plotting).

Here are the results for estimating the means of each of the 30 variables (numbered 1 to 30 by decreasing standard deviation), for HMC with trajectory lengths of 100, 170, and 200 leapfrog steps (and hence trajectory lengths of about 163, 277, and 326 time units since the stepsize is about 1.63):

The left plot gives the variances of the estimates, not accounting for computation time; the right plot adjusts for computation time (gradient evaluations). Smaller is better in both plots. Note that the vertical scale is logarithmic, with horizontal lines at each power of ten.

These results look rather peculiar! Notice how the variances of the mean estimates for variables 3 to 28, with standard deviations declining from 16 to 8, don’t decline as one might expect, but rather go up and down, with peaks at positions that change with the trajectory length.

This behaviour is due to a phenomenon discussed in Section 3.2 of my review of Hamiltonian Monte Carlo. Hamiltonian dynamics for this simple distribution without dependencies between variables will be periodic for each variable. If the period for a variable happens to match (or be near) the trajectory length, the end-point of a trajectory will be close to the start point, with the result that sampling for that variable is very poor. (A related problem  happens when the trajectory length is half the period.) Note that this problem can arise for any multivariate normal distribution, with the poorly-explored directions being the eigenvectors of the covariance matrix, not necessarily the individual variables.

The cure for this is to randomly vary the trajectory length (randomly varying the stepsize, or the number of leapfrog steps, or both) over some moderate range. I modified the hmc_da function in the NUTS software to do this, changing the computation of the number of leapfrog steps from

L = max(1, round(lambda / epsilon));

to

L = max(1, round((0.9 + rand/5) * lambda / epsilon));

which has the effect of multiplying the number of leapfrog steps by a random factor uniformly distributed between 0.9 and 1.1.

Here are the results after this modification:

The variances of the mean estimates still go up and down a bit (maybe a wider random range would be better), but much less than before.

So we see that one can get a misleadingly-bad impression of the performance of HMC on a multivariate normal distribution from experiments in which the trajectory length is not varied randomly . On less simple distributions, the exact periodicities that happen with a multivariate normal may not be present, but there can be approximate periodicities, which might still happen to nearly match a fixed trajectory length, with a consequent bad effect on performance. This is why randomly varying the trajectory length is a recommended part of standard HMC methodology. (However, this is unnecessary with “windowed” HMC, as long as the window size is a non-negligible fraction of the trajectory length.)

So, how does NUTS perform on this distribution? Here are the results, together, for comparison, with the variances of mean estimates from an equal-size sample of points drawn independently (omitted for the computational cost plot, where it would not be meaningful):

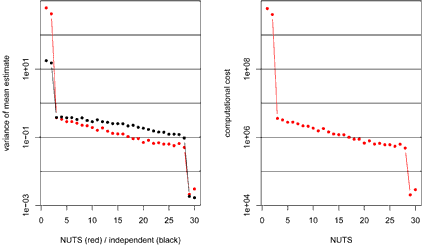
For the first two variables, with the largest standard deviations, the variances of the NUTS estimates of the mean are about 30 times bigger than the variances when the sampled points are independent.  Compared to HMC with random trajectory length with median 200, these NUTS estimates have a variance that is about 25 times bigger. After adjusting for computational cost, the NUTS estimates of the means of these two variables are 7 times less efficient than the HMC estimates.

NUTS looks much better for the other variables, with smaller standard deviations. Indeed, the NUTS estimates are often better than those obtained with independent sampling! This is possible because NUTS (and HMC) can produce negative autocorrelations. However, for negative correlations to show up with these variables, NUTS must often be using trajectories that are much shorter than are needed for efficient exploration of the large-standard-deviation variables, which of course is consistent with it estimating the means of those variables inefficiently.

Here are plots showing the performance of HMC with random trajectory length and of NUTS when estimating the variances (rather than the means) of the 30 variables:

HMC is about a factor of two more efficient than NUTS at estimating the variances of the two variables with the largest standard deviations, but is less efficient at estimating the variances of the other variables.

One might think that these results show that there’s a tradeoff — HMC better for variables with large standard deviation, NUTS better for variables with small standard deviation. But I think this isn’t really so. First, it is often the absolute magnitude of the variance of estimates that is important, and in that respect HMC is clearly better. (Consider, for instance, estimating regression coefficients for covariates that have been standardized.) When that’s not so — when you need precise estimates of the means of variables that have small standard deviations — it’s easy to alternate HMC updates designed to sample well for the variables with large standard deviations with other, much cheaper, updates designed to sample well for the variables with small standard deviations (eg, univariate slice sampling updates, or just HMC with a smaller trajectory length). Using the windowed HMC method would also help, since rejected transitions in windowed HMC will usually move a small distance, helping with the sampling for variables with small standard deviations. (Note: as mentioned before, due to the rotational invariance of HMC, all this discussion applies also when the “variables” are actually various directions in the space, that aren’t necessarily the coordinate axes being used.)

One conclusion I draw from this evaluation is that the better performance of NUTS over HMC (optimally tuned) shown in the evaluations in the NUTS paper is likely an artifact of not randomizing the HMC trajectory length, and of evaluating performance by the worst effective sample size for any variable (not accounting for some variables being easy to handle by other methods). Another conclusion is that the premature U-Turn problem that I discussed in my first post on NUTS can be a problem in practice, since otherwise NUTS would estimate the means and variances of the large-standard-deviation variables in this example better. As I discussed there, I think there is scope for improving the way that NUTS decides when to stop a trajectory, and thereby make it a more generally-useful sampling method.